고장률의 형태별 대응 분포

 

 

 2.2  고장률의 형태별 대응 분포

 2.2.1   CFR과 지수분포

개개의 부품에 대한 고장시간의 분포(수명분포)는 지수분포에 따른다고 알려져 있다. Drenick의 정리에 따르면  개개 부품의 수명분포가 지수분포가 아니더라도 시스템의 수명분포는 비교적 넓은 조건하에서 근사적으로 지수분포가 된다. 

그리고 고장확률밀도함수가 지수분포에 따르면 고장률은 CFR이 된다. 고장까지의 시간의 분포가 지수분포인 경우의 고장확률밀도함수 는 다음 식과 같다.

    여기서 는 평균고장률로서

외 관계가 있다.는 평균고장간격시간(Mean Time Between Failure)으로서, 평균수명이 된다. 평균수명을 로 표시하면 가 되고, 식(10.19)는

으로 표시되기도 한다.

지수분포인 경우의 신뢰도함수 , 누적분포함수 , 고장률함수 는 다음과 같이 된다. 

지수분포의  의 관계곡선은 제3장의 〔그림 3-9〕를 참조 바란다.

 

 평균고장시간() 6,000시간을 갖는 기구가 360시간에서의 신뢰도는 얼마인가를 구하라.

〔풀이〕이 분포는 지수분포를 한다.

    신뢰도

    이므로 신뢰도는 6.18%가 된다.

 

2.2.2   IFR과 정규분포

계량치의 분포는 정규분포를 한다고 알려져 있다. 따라서 재료의 인장강도와 같이 사용시간 또는 사용회수의 증가에 따라 고장수가 증가하게 되는 부품 또는 시스템의 고장(즉 증가형 고장률 또는 IFR인 경우의 고장)확률밀도함수도 정규분포를 하게 된다.

정규분포인 경우의 고장확률밀도함수 와 누적분포함수 및 신뢰도함수 는 다음과 같다.

         

또한 인 표준화 정규분포의 경우 는 다음과 같이 되는데, 일반적으로 이것을 많이 사용한다.

여기서, 는 로 되고, 이면 로 되어 부터 까지의 적분으로 된다. 한편 는 다음 식으로도 표현된다.

그리고 는 다음과 같이 된다.

 어떤 부품의 고장시간의 분포가 사이클, 사이클인 정규분포를 한다면 사이클일 때의 신뢰도 와 순간고장률 는 얼마인가.    

〔풀이〕

와 의 관계 및 신뢰도 는 다음과 같다.

여기에서 는 

이고, <부표 23>의 정규확률분포와 <부표 24>의 정규누적분포표에 의거하면

가 된다. 따라서 사이클일 때의 신뢰도와 순간고장률은 다음과 같다.

가 되고, 순간고장률는 의 관계로부터

가 된다. 여기에 값을 대입하면

     

2.2.3   와이블분포

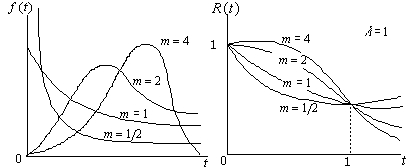
고장확률밀도함수 가 지수분포를 따르는 경우 고장률함수「일정」이 되고, 고장확률밀도함수가 정규분포를 따르는 경우 고장률함수는 증가형이 된다. 즉, 고장확률밀도함수 에 따라 고장률함수의 분포가 달라진다.

일반적으로 고장률함수의 분포에는 ① 감소형 고장률(DFR-decreasing failure rate) , ② 일정형 고장률(CFR-constant failure rate) , ③ 증가형 고장률(increasing failure rate) 의 3가지가 있다. 

따라서 고장률함수의 분포에 따라 적절하게 고장확률밀도함수를 표현할 수 있도록 만든 확률분포가 필요한데 이것이 스웨덴의 Waloddi Weibull이 고안한 와이블분포이다.

와이블분포는 다음 식들과 같이 표현되며, 여기서 은 형상모수(shape parameter), 는 척도모수(scale parameter)  그리고 는 위치모수(position parameter) 라고 부른다.

     

척도모수 는 의 관계로부터 

로 변형되므로 윗 식(10.31)∼(10.34)들은

등과 같이 변형된 식으로 될 수 있다. 형상모수 은 분포의 형을 결정하는 모수로서

① 이면 고장률함수는 감소형 고장률(DFR)에 대응한다.

② 이면 고장률함수는 일정형 고장률(CFR)이 되고 고장확률밀도함수는 지수분포에 대응한다.

③ 이면 고장률함수는 증가형 고장률(IFR)이 되고, 고장확률밀도함수는 정규분포(일 때)에 대응한다.

이면

이고, 사용시간 이면 에 관계없이   

 즉, 사용시간 만큼 사용되면 37%가 잔존하고, 63%는 이미 한 번 이상 고장을 경험한 것이 된다. 여기서 37%가 잔존하는 시간을「특성수명  」이라고 한다.한편 와이블분포의 와를 각종의 의 값에 따라 그래프로 그려보면 다음〔그림 10-4〕와 같다.

〔그림 10-4〕와이블분포의 와  

그리고 평균수명 와 평균수명의 분산 를 와이블분포에 의거하여 구하면 다음과 같이 된다.

상기 식들을

를 써서 바꾸어 표현하면 다음과 같다.

             

     

  어떤 자동차부품의 수명분포는 인 와이블분포에 따르고 있다. 이 부품의  주행시 생존할 확률을 구하라. 

〔풀이〕생존확률은 신뢰도이므로 을 구하면

가 된다. 즉, 77.4(%)가 생존한다.

[주의] 통계 관련 각종 분포의 부호는 종종 바뀌므로 최신 부호 적용(KS규격이 기준)에 유의바랍니다.

radial_purple.gif 출처 :  품질기술사 수험도서  통계적품질관리      radial_purple.gif 출판사 : (주)ATPM컨설팅

radial_purple.gif 저자 :  공학박사/기술사/지도사 권오운


                    QM/SQC분야 자료실  메인 페이지로              자료실 메인으로

Copyright ⓒ ATPM Consulting Inc. All Rights Reserved.